上一篇我们说到了“码间串扰”，还留下了一个问题，那就是如何在不降低信号带宽的情况下，克服码间串扰的影响，顺便再获得点“频率分集”增益呢？今天我们就来聊聊这些话题。

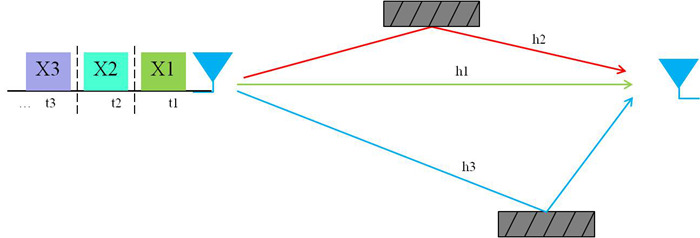
    来看图1描述的传播环境，假设从发送方到接收方一共有三条传播路径，信道增益分别为h1，h2和h3。其中路径2和3分别会对信号延时1个和2个时刻。即，在第一时刻，接收方会收到经过直视径到达的信号X1（不考虑噪声） ：

    第二时刻，接收方收到来自直视径的X2和经反射径1延时到达的X1：

    可以看到，码间串扰已经发生。同理，在第三时刻，接收方收到的信号是

    以此类推。熟悉“信号系统”的朋友一眼就看出来了，这其实就是输入序列X=[X1，X2，X3…]与信道响应h=【h1  h2  h3 】做了一个卷积，Y = h * X。所以卷积是描述多径传播最漂亮的数学表达。但是卷积的表达式仍然太繁琐，我们不妨来做一个转换。
    我们把上面描述的传播环境想象成一个3发1收的MISO系统，那么，上述3条多径信道响应【h1  h2  h3 】就可以看成从3根发送天线分别到接收天线间的直视信道响应，如图2所示。我们设计以下的发送策略：第一时刻，从天线1发送符号X1，这时，接收端收到的就是：

    第二时刻，从天线2发送X1，从天线1发送X2，接收信号是：

    第三时刻，从天线3发送X1，天线2发送X2，天线1发送X3，我们有：

    以此类推。很明显，这与卷积的表达式一模一样。现在我们把具有码间串扰的多径传播环境转换成了熟悉的多天线MISO系统，形式上比较好理解，更重要的是，我们可以使用多天线的技术来处理码间串扰了。

 

    在着手“干掉”码间串扰之前，我们先来看一个有趣的例子，帮助我们直观的理解消除码间串扰时，所采用的思想。
    正月十五，笔者和爸爸妈妈去看灯展。这次灯展，有三盏最漂亮的大花灯并排放在最显眼的展台上。笔者很想去展台上和三盏灯合影，但参观的人实在是太多了，管理员不得不做出以下规定：所有人排成一排，按顺序从入口上展台，每盏灯前面只能站一人，照完相后，从出口依次离开，每出去一人，就进来一人。
    于是，笔者就去排队了，爸爸妈妈在台下给笔者照相。当某一时刻，笔者走上展台，站在第一盏灯前的时候，其他灯前的游客还没有离开，笔者和三盏灯的合影就有了别人在旁边“抢镜”。同样，在后面两个时刻，有人出就有人进，笔者始终无法单独和三盏灯来一次完美的合影，甚是郁闷。

图3 笔者受到其他人干扰，无法和三盏灯合影

    当然，这点小事难不倒笔者，我想，既然没有办法单独和三盏灯合影，那么与其身边站着其他人，不如和自己人一起照。于是笔者把相机交给好心人，拉着爸爸妈妈一起去排队了。这一次，虽然刚上展台的时候，有游客干扰，但是总有一个时刻，展台上只有笔者和爸爸妈妈三人，我们开开心心的来了一张合影。
    此时笔者玩心大发，一张合影还不满足，笔者想分别站在三盏灯下，和爸爸妈妈来三张合影。于是笔者拉着爸爸妈妈又一次去排队了。这次，当笔者站在第3盏灯下和爸爸妈妈完成第一张合影后，迅速从出口跑出，绕回入口，紧跟着妈妈再次登上展台（可爱的管理员也不忍心阻止笔者的行动），这样，笔者就在第一盏灯下，又来了一张合影；紧接着，笔者的爸爸也迅速绕回入口，跟在笔者后面再次上了展台，就这样，我们完成了分别在三盏灯下合影三次的愿望。

    看完上面的例子，大家是不是已经被笔者“绕”晕了？呵呵，没关系，我们只要知道笔者是如何“挤”掉其他人，让台上只有我们三人，并且如何通过“循环”入场，获得三次合影机会的，就可以了。因为无线通信中，“干掉”码间串扰，用的也是这两招：
    （1）把连续多个符号看成一组，一起进行处理，“挤”开码间串扰。这样码间串扰就只会发生在开头和最后的几个符号上，中间的都是“自己人”，不受影响。
    （2）通过在这一组符号的开头或最后设置“循环前缀”，干掉码间串扰。
    我们把这两招用数学语言，重新进行描述。仍然考虑开篇的传播环境，这次我们把X1，X2，X3看成一组，并在前面加上“循环前缀”X2，X3，形成【X2，X3，X1，X2，X3 】。然后与信道响应【h1 h2  h3】进行卷积，过程如下：

    我们一共能得到7个时刻的方程，但最后两个说的是本组符号对下一组符号造成的干扰，那就留给下一组符号去解决吧。我们只看前5个时刻。很明显，码间串扰发生在前两个时刻Y1，Y2（信道矩阵中0元素的位置就是干扰符号出现的位置，因为我们没有把干扰符号写进方程，所以该位置是0）。没关系，受到干扰的符号我们删掉，不要了。剩下三个时刻的方程，我们仔细一看，这不就是一个3发3收的MIMO传输方程么？我们曾经把多径传播环境转换成了MISO系统，现在又转换成了MIMO系统！

    说到MIMO系统，我们太熟悉了，至少，我们也花了三大篇文章详细的解释过了。还记得“知己知彼，百战不殆--信道信息的获取和应用”中我们介绍的内容么？MIMO系统的最佳传输矩阵是什么？没错，是对角阵。怎样才能获得对角阵呢？对信道矩阵H进行SVD分解，得到H=U·S·V，其中S就是对角矩阵；接下来，就是用V的共轭转置V*对发送信号进行“预编码”，接收端在收到数据后，同样乘以U*，这样一来，发送的符号就像进入了独立平行的正交子信道，互不干扰。（对这部分内容不熟悉的朋友可以在本论坛内找到“知己知彼，百战不殆--信道信息的获取和应用”。）

    现在我们拿到了一个等效的3x3 MIMO传输系统，当然也可以按照上述过程来处理它。于是，我们对信道矩阵H进行SVD分解----此时此刻，本文最大的悬念就要揭晓了----注意矩阵H的特殊结构，因为我们对发送数据添加了循环前缀，所以H的每一行就有一个“循环位移”，拥有这种“循环位移”结构的矩阵叫做“循环矩阵（Circulant Matrix）”。循环矩阵的一个重要特性就是：对它进行SVD分解后，得到的左酉阵U是“逆傅里叶变换矩阵”（我们用W-1来表示，即U = W-1）；而右酉阵V是“傅里叶变换矩阵”（V = W，注：一组数据乘以“傅里叶变换矩阵”，就相当于对该组数据进行了傅里叶变换，并且有W-1W= WW-1=I）！

    这就是说，如果我们对一组数据先进行 “逆傅里叶变换”，添加“循环前缀”，再送入多径信道；接收端删除掉受干扰的“循环前缀”后，做一个“傅里叶变换”，得到的数据就好像经过了独立平行的正交子信道，彼此之间不受任何干扰。而整个这一套处理流程，不正是“OFDM”么？呵呵，我们一整篇文章好像都在说MIMO，直到最后时刻才让OFDM出场，OFDM同学一定等急了吧？
    我们来梳理一下OFDM的处理流程：首先，对一组发送符号进行“逆傅里叶变换”--相当于MIMO系统中的“预编码”；然后，添加“循环前缀”--为的是让传输矩阵H变成“循环矩阵”，最后送入多径信道；接收端舍弃受到干扰的“循环前缀”--码间串扰就这样被干掉了；再做一个“傅里叶变换”--相当于MIMO中对接收信号乘以U*；得到的符号就像经过了互不干扰的正交子信道。

    通过这样的类比，我们猛然发现，“原来OFDM其实也是MIMO啊”。两者的区别在于：MIMO中，对信道H进行SVD分解，需要知道H具体内容；而在OFDM中，预编码矩阵（即“逆傅里叶变换矩阵”）不依赖于H。笔者本来想把这句话写在文章的开头，害怕被拍砖，最后决定还是放在后面吧。不过读到这里，相信大家也跟笔者有了同样的感受了吧？至少，我们从另一个角度诠释了OFDM的意义。
    顺便一提，在“灯展”的例子中，笔者实现了在三盏灯下分别合影的愿望，而在OFDM系统中，每个发送符号都和h1 h2 h3相乘过，就是说，我们还获得了一定的“频率分集增益”哦。
    既然OFDM 与MIMO有如此深的渊源，而且本回中，并未介绍OFDM相关参数的含义，比如OFDM符号长度，子载波间距等。下一回，我们就来看看OFDM与MIMO联合使用时，会有什么效果？如果我们要设计一个OFDM系统，它的参数应该怎么选取呢？


    闲话：OFDM是“多载波”技术的一种，在单载波系统中，如果要消除码间串扰，就要用到著名的“维特比算法”。关于算法的具体步骤，本文不再赘述。在计算机和互联网领域，维特比算法有着更广泛的应用，比如“语音识别”，“中文输入法”等。对互联网技术感兴趣的朋友也可以阅读吴军老师的“数学之美”。